Reynold's Experiment
• Osborne Reynolds (Mathematician & Physicist, UK)
• In 1883, he developed a laboratory set up in which he injected Dye (i.e. a fine, threadlike stream of colored liquid having the same density as water) at the entrance to a large glass tube through which water was flowing from a tank.
 |
| Fig: Reynold's experiment |
• Procedure:
✓ The water from the tank was allowed to flow through glass tube into atmosphere.
✓ The velocity of flow was varied by the valve.
✓ Dye was injected into the flow through a small tube.
• Observation:
✓ At the initial stage of flow, dye filament in the glass tube was in the form of straight line. This was a laminar flow.
✓ When increasing the velocity of flow, the dye filament was no longer a straight line. The dye filament starts to become wavy. This was a transitional flow.
✓ While further increase in velocity of flow, the wavy dye filament broke up and finally diffused in water. This was a turbulent flow.
✓ The occurrence of a laminar and turbulent flow was governed by the relative magnitude of inertia and viscous force. For low velocities, viscous force is predominant whereas for higher velocities, inertia force is predominant.
Where,
V= Mean velocity, u= Coefficient of Kinematics viscosity = μ/p,
μ= Coefficient of Dynamic viscosity = up, p= Density of fluid,
L = Characteristics length, L= Diameter of Pipe (D), in pipe flow
Laminar Flow in Circular Pipe
Assumptions: incompressible, steady, developed laminar flow in a circular pipe.
A horizontal pipe of radius 'R' through which a fluid of density 'p' flows.
Let us consider, a fluid element with having radius 'r' of length 'dx' in the direction of flow.
Here,
p = Pressure intensity
't= Shear stress on the periphery of the cylinder acting in opposite direction of flow.
Forces acting on the fluid element: Pressure force, Shear force and Component of weight.
 |
| Fig: Forces acting on a fluid element |
Ad:
- Pipe flows and open channel flows in Hydraulics
Turbulent Flow | Velocity and shear stress in turbulent flow
Interception and Interception losses
Turbulent Flow | Velocity and shear stress in turbulent flow
Hydrodynamically smooth and rough boundaries | Velocity distribution for turbulent flow
Nikuradse experiment | variation of frictional factor (f) for laminar and turbulent flow
Velocity distribution in smooth pipes | Velocity distribution in rough pipes
- Determination of Value of 'f' from Moody's Chart
Minor head losses in pipes | Equivalent length of pipe representing minor head losses
Syphon and its application
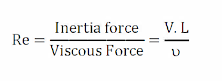





Comments
Post a Comment