Skip to main content

Determination of Value of 'f' from Moody's Chart | Hydraulics

 Moody's Diagram (or Moody's Chart)



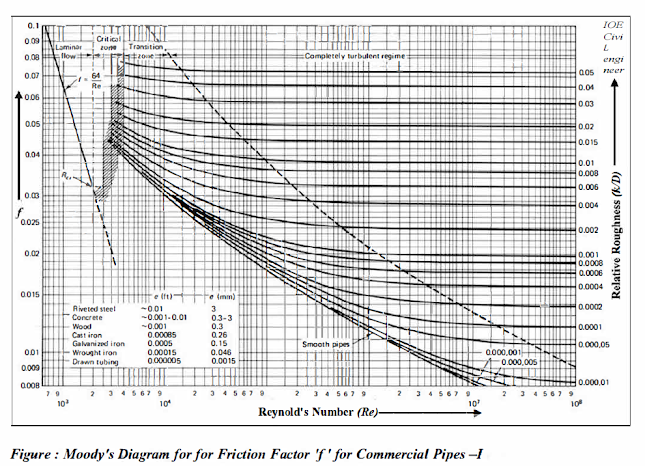Fig: Moody's diagram for the friction factor 'f' for commercial pipes-I



L.F. Moody has plotted the equation as shown in above figures, commonly known as 'Moody Diagram' which is essentially the same as thet of Nikuradse's plot except for the transition regions. So, 'Moody chart' is the chart of friction factor 'f' versus 'Re' curves for various values of 'R/k'.
For any turbulent pipe flow problem the value of friction factor (f) can therefore be determined from
Moody's Diagram  if the numerical values of 'R/k' for the pipe and 'Re' of flow are known. The values of 'k' which may be adopted for the pipes of some of the common materials are given below


Ad:

https://happyshirtsnp.com/



Fig: Moody's diagram for friction factor 'f' for commercial pipes-II



The value of Equivalent sand grain roughness (k)' given in Table 1-2 correspond to material in new and clean condition. As the pipe become older, the roughness increases may increase with time in accordance with following expression



Where, k= Equivalent sand grain roughness at any time 't', Equivalent sand grain roughness of new pipe material and a = Time rate of increase of roughness.

Salient features of Moody's Diagram

a) Laminar flow (Re<2000)

Friction factor (f) is a function of 'Re' only


b)                Critical zone (2000<Re<4000)

Flow in this zone is either laminar or turbulent (i.e. oscillatory flow that alternately exists between laminar and turbulent flow). There is no any specific relationship between 'f 'and 'Re' in this zone.


c)                Transition zone (Re>4000)

For 'k/D < 0.001 ' and certain ranges of 'Re' in this zone, the roughness elements are submerged in the viscous sub-layer, and the flow can be considered to be smooth pipe flow. In this zone, T is a function of both 'Re' and 'k/D'.


d)                Complete turbulent zone (Re>4000)



In this zone, average roughness height is substantially greater than the viscous wall layer thickness. As 'Re' is high, the head loss is also higher due to the extra turbulence caused by projections. The friction factor (f) is a function of 'k/D' only and is independent of 'Re'. The horizontal lines indicate that friction factor (D does not change with 'Re', that means viscosity does not affect the head loss in this zone.


Determination of Value of 'f' from Moody Chart:



(i)               Mark the value of 'Re' =VD/v on the abscissa (i.e. Re - axis)

(ii)             For the given value of 'k/D', mark the point of intersection of 'Re' with 'k/D'. To find the intersection point, draw vertical line from 'Re' and follow curve path from 'k/D'. If 'k/D' curve is not available for given value of 'k/D', draw a curve by following the trend of nearby curve.

iii) Draw a horizontal line from the point of intersection of 'Re' and 'k/D' to ordinate (i.e. f- axis) 

(iv)               Finally, read the value of friction factor (D from the chart.



                                                 Flow chart of Friction factor (f)

Flow chart for friction factor 'f'




Friction factor (f) can be calculated either from Resistance Equations or by using Moody Chart as in Figure. When Moody Chart is not given then use the Resistance Equations to calculate the friction factor (f).



Ad:



Read more:


Labels:
Location: Kathmandu 44600, Nepal

Comments

Post a Comment

Popular posts from this blog

Hydrodynamically smooth and rough boundaries | Velocity distribution for turbulent flow

 Hydrodynamically smooth and rough boundaries Fig: Definition of smooth and rough boundaries In general, a boundary with irregularities of large average height 'K' on its surface is considered to  be a rough boundary and one with smaller 'K' value is considered as a smooth boundary. ✓ However, for a proper classification of smooth and rough boundaries, the flow and fluid characteristics are required to be considered in addition to the boundary characteristics. ✓ As the flow outside the laminar sub-layer is turbulent, eddies of various sizes are present which try  to penetrate through the laminar sublayer. But, due to greater thickness of laminar sub-layer ,   eddies can't reach the surface irregularities and thus the boundary acts as a smooth boundary. Such  a boundary is termed as " Hydro-dynamically Smooth Boundary" ✓ With the increase in Reynold's no (Re), the thickness of the laminar sub-layer  decreases and it's  can even become much smaller ...
Post a Comment
Read more

Water hammer and unsteady flows in pipes

             Ad: https://happyshirtsnp.com/                                                                             UNSTEADY FLOW IN PIPES When water is flowing through a pipe is suddenly stopped by the use of valve then we can see sudden rise in pressure inside the pipe and this pressure waves transmitted along the length of the pipe and it creates knocking like sound effects knows as 'water hammer'. In doing so, there are rapid pressure oscillation in the pipe, often accompanied by a hammering like sound, this phenomenon is called as 'Water hammer effect'. Sometimes the pressure may rise to the greater extent and may causes serious damage to the pipe. Therefore the 'water hammer' effects should be properly studied in the pipes. The magnitude of pressure rise d...
Post a Comment
Read more

Reynold's Theory | Prandtl mixing length Theory

                                         Reynold's Theory Fig: Transfer of momentum in turbulent flow Relative velocity of layer 'A' w.r.t. layer 'B' is So, fluctuating components in X and Y directions due to turbulence are Vx and Vy . Now if over a surface of area 'A' perpendicular to the Y-direction and separating two adjacent fluid layers the component 'Vy ' is uniformly distributed.  So, Mass of fluid transferred across that surface from one layer to another per second =                                                        pAVy This mass of fluid has started moving with a relative velocity 'Vx'. So, Transfer of momentum = pAVxVy takes place, resulting in developing tangential forces on each of the layers. Now, the corresponding turbule...
Post a Comment
Read more